AC 自动机

AC 自动机 = $\text{trie}$ + $\text{kmp}$ 的思想

AC 自动机

问题：给定 $n$ 个模式串和一个文本串，问有多少个模式串出现在文本串中

跑 $n$ 遍 $\text{kmp}$ ？若数据毒瘤会超时

于是一些珂学家们发明了 AC 自动机

fail

假设模式串分别是 he she her shy say

建出 $\text{trie}$ 树

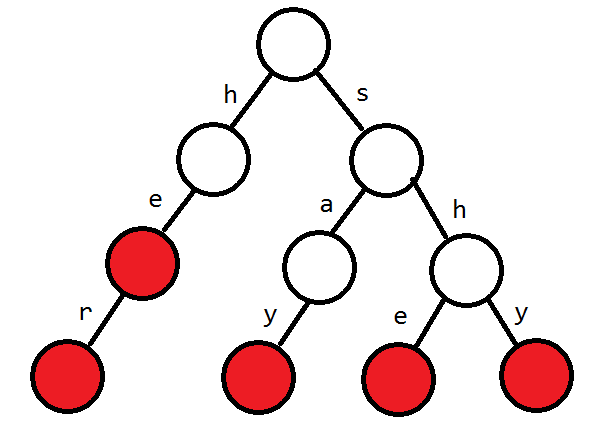
暴力匹配效率不高，考虑用 $\text{kmp}$ 的 $next$ 思想，在 $\text{trie}$ 上建一个 $fail$

设当前串 $S$ 以 $u$ 结尾，则 $fail_u$ 指向

能与 $S$ 后缀匹配的）最长的） $\text{trie}$ 的前缀所在的）节点

这着实有点绕，可以康康图

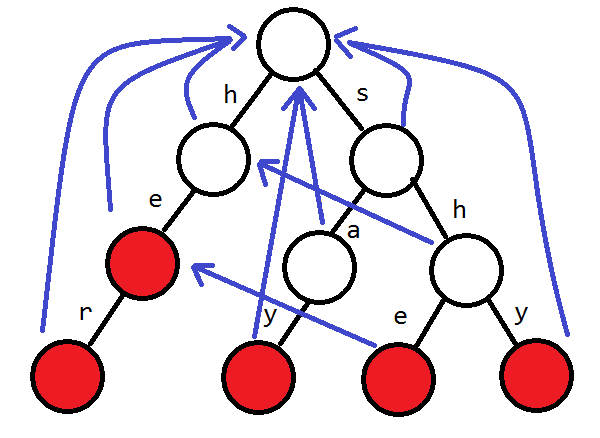
如图，能与 she 的后缀匹配的 $\text{trie}$ 的前缀，只有 he

如何构建

考虑 bfs ，对于当前点 $u$ 存在的儿子 $ch_{u,i}$

从 $u$ 开始往上跳 $fail$ ，直到一个点 $v$ 也有 $ch_{v,i}$ ，那么 $ch_{u,i}$ 的 $fail$ 指向 $ch_{v,i}$

特别的，如果没有符合条件的 $v$ ，那么 $fail$ 指向根

同时第二层的 $fail$ 都指向跟

inline void gfail() {
	for(int i=0;i<26;i++)
		if(ch[0][i])q[++tl]=ch[0][i];
	register int u;
	while(hd<tl) {
		u=q[++hd];
		for(int i=0,v;i<26;i++) {
			if(ch[u][i]) {
				v=fail[u];
				while(!ch[v][i] && v)v=fail[v];
				fail[ch[u][i]]=ch[v][i];
				q[++tl]=ch[u][i];
			}
		}
	}
}

查询

如何查询文本串 $s$ 呢

指针 $u$ 从根开始，将每个字母送入自动机

若不存在 $ch_{u,c}$ ，则跳 $fail$ 找到一个存在的 $ch_{v,c}$

然后沿着从 $fail$ 到根的路径统计个数，

注意不要重复

inline int ask(int le) {
	register int u=0,ans=0;
	for(int i=1,v;i<=le;i++) {
		v=s[i]-'a';
		while(!ch[u][v] && u)u=fail[u];
		u=ch[u][v];
		for(int j=u;j && flg[j];j=fail[j])
			ans+=flg[j],flg[j]=0;
	}
	return ans;
}

trie 图

发现如果当前节点没有对应的子节点，那么就需要沿着 $fail$ 向上走，会浪费时间

考虑在建立 $fail$ 时补全 $\text{trie}$ 树，形成 $\text{trie}$ 图

若 $u$ 不存在儿子 $i$ ，则将儿子 $i$ 指向 $fail_u$ 儿子 $i$

否则直接将儿子的 $fail$ 指向 $fail_u$ 的儿子 $i$

inline void gfail() {
	for(int i=0;i<26;i++)
		if(ch[0][i])q[++tl]=ch[0][i];
	register int u;
	while(hd<tl) {
		u=q[++hd];
		for(int i=0;i<26;i++) {
			if(ch[u][i]) {
				fail[ch[u][i]]=ch[fail[u]][i];
				q[++tl]=ch[u][i];
			} else ch[u][i]=ch[fail[u]][i];
		}
	}
}

匹配完后的查询也不需要跳 $fail$ 了

inline int ask(int le) {
	register int u=0,ans=0;
	for(int i=1;i<=le;i++) {
		u=ch[u][s[i]-'a'];
		for(int j=u;j && flg[j];j=fail[j])
			ans+=flg[j],flg[j]=0;
	}
	return ans;
}

Code

例：模板

#include<bits/stdc++.h>
using namespace std;
const int N=1000005;
int n,ch[N][26],fail[N],flg[N],tot,hd,tl,q[N];
char s[N];
inline void ins(int le) {
	register int u=0;
	for(int i=1,v;i<=le;i++) {
		v=s[i]-'a';
		if(!ch[u][v])ch[u][v]=++tot;
		u=ch[u][v];
	}
	flg[u]++;
}
inline void gfail() {
	for(int i=0;i<26;i++)
		if(ch[0][i])q[++tl]=ch[0][i];
	register int u;
	while(hd<tl) {
		u=q[++hd];
		for(int i=0;i<26;i++) {
			if(ch[u][i]) {
				fail[ch[u][i]]=ch[fail[u]][i];
				q[++tl]=ch[u][i];
			} else ch[u][i]=ch[fail[u]][i];
		}
	}
}
inline int ask(int le) {
	register int u=0,ans=0;
	for(int i=1;i<=le;i++) {
		u=ch[u][s[i]-'a'];
		for(int j=u;j && flg[j];j=fail[j])
			ans+=flg[j],flg[j]=0;
	}
	return ans;
}
int main() {
	scanf("%d",&n);
	for(int i=1;i<=n;i++) {
		scanf("%s",s+1);
		ins(strlen(s+1));
	}
	gfail();
	scanf("%s",s+1);
	printf("%d",ask(strlen(s+1)));
}

例：查询出现个数，一样的题

#include<bits/stdc++.h>
using namespace std;
const int N=1000005;
int n,ch[N][26],mx,ans[N],fail[N],flg[N],tot,hd,tl,q[N];
char s[N],st[200][200];
inline void ins(int le,int id) {
	register int u=0;
	for(int i=1,v;i<=le;i++) {
		v=st[id][i]-'a';
		if(!ch[u][v])ch[u][v]=++tot;
		u=ch[u][v];
	}
	flg[u]=id;
}
inline void gfail() {
	for(int i=0;i<26;i++)
		if(ch[0][i])q[++tl]=ch[0][i];
	register int u;
	while(hd<tl) {
		u=q[++hd];
		for(int i=0;i<26;i++) {
			if(ch[u][i]) {
				fail[ch[u][i]]=ch[fail[u]][i];
				q[++tl]=ch[u][i];
			} else ch[u][i]=ch[fail[u]][i];
		}
	}
}
inline void ask(int le) {
	register int u=0;
	for(int i=1;i<=le;i++) {
		u=ch[u][s[i]-'a'];
		for(int j=u;j;j=fail[j])
			ans[flg[j]]++;
	}
}
int main() {
	scanf("%d",&n);
	while(n) {
		memset(ch,0,sizeof(ch));
		memset(flg,0,sizeof(flg));
		memset(ans,0,sizeof(ans));
		for(int i=1;i<=n;i++) {
			scanf("%s",st[i]+1);
			ins(strlen(st[i]+1),i);
		}
		gfail();
		scanf("%s",s+1);
		ask(strlen(s+1));
		mx=0;
		for(int i=1;i<=n;i++)mx=max(mx,ans[i]);
		printf("%d\n",mx);
		for(int i=1;i<=n;i++)
			if(ans[i]==mx)printf("%s\n",st[i]+1);
		scanf("%d",&n);	
	}
}

Fail 树

用途：统计模式串出现的个数

和加强版很想？可是暴力跳巨慢？

想想匹配的过程，从头开始跳 $fail$ ，期间到的每个点都是一个出现的串

既然可以一个一个顺着跳，同理从模式串结尾往上跳到的节点个数就是该串出现的次数

于是可以只留下反着的 $fail$ 边，形成 $fail$ 树

只要将属于文本串的节点标为 1 ，那么节点 $u$ 的子树和就是 $u$ 出现的次数

子树和可以用 $\text{dfs}$ 序+树状数组，复杂度下降许多

例：几乎一样的题

#include<bits/stdc++.h>
using namespace std;
const int N=2000005;
int n,len,ch[N][26],fail[N],flg[N],tot,hd,tl,q[N],sz[N],tr[N];
char s[N];
int lst[N],nxt[N],to[N],cnt,dff,dfn[N];
inline void Ae(int fr,int go) {
	to[++cnt]=go,nxt[cnt]=lst[fr],lst[fr]=cnt;
}
inline void ins(int le,int id) {
	register int u=0;
	for(int i=1,v;i<=le;i++) {
		v=s[i]-'a';
		if(!ch[u][v])ch[u][v]=++tot;
		u=ch[u][v];
	}
	flg[id]=u;
}
inline void gfail() {
	for(int i=0;i<26;i++)
		if(ch[0][i])q[++tl]=ch[0][i];
	register int u;
	while(hd<tl) {
		u=q[++hd];
		for(int i=0;i<26;i++) {
			if(ch[u][i]) {
				fail[ch[u][i]]=ch[fail[u]][i];
				q[++tl]=ch[u][i];
			} else ch[u][i]=ch[fail[u]][i];
		}
	}
	for(int i=1;i<=tot;i++)
		Ae(fail[i],i);
	
}
void dfs(int u) {
	dfn[u]=++dff,sz[u]=1;
	for(int i=lst[u],v;i;i=nxt[i])
		dfs(v=to[i]),sz[u]+=sz[v];
}
inline void add(int p,int v) { for(;p<=dff;p+=p&-p)tr[p]+=v; }
inline int ask(int p) { register int s=0; for(;p;p-=p&-p)s+=tr[p]; return s; }
inline int tree(int u) { return ask(dfn[u]+sz[u]-1)-ask(dfn[u]-1); }
int main() {
	scanf("%d",&n);
	for(int i=1;i<=n;i++) {
		scanf("%s",s+1);
		ins(strlen(s+1),i);
	}
	gfail(),scanf("%s",s+1),len=strlen(s+1);
	dfs(0);
	for(int i=1,u=0;i<=len;i++)u=ch[u][s[i]-'a'],add(dfn[u],1);
	for(int i=1;i<=n;i++)printf("%d\n",tree(flg[i]));
}

一些灵活应用

可以通过反向 $\text{dfs}$ 序实现 $O(n)$ 求出答案

把队列反向枚举，然后把 $fail_u$ 的答案加上 $u$ 的答案

因为 $\text{bfs}$ 满足深度的递增

// https://gmoj.net/senior/#main/show/4328
// https://gmoj.net/senior/#main/code/808016
#include<bits/stdc++.h>
using namespace std;
const int N=2000005;
int n,len,ch[N][26],fail[N],flg[N],tot,hd,tl,q[N],sz[N];
char s[N];
inline void ins(int le,int id) {
	register int u=0;
	for(int i=1,v;i<=le;i++) {
		v=s[i]-'a';
		if(!ch[u][v])ch[u][v]=++tot;
		u=ch[u][v];
	}
	flg[id]=u;
}
inline void gfail() {
	for(int i=0;i<26;i++)
		if(ch[0][i])q[++tl]=ch[0][i];
	register int u;
	while(hd<tl) {
		u=q[++hd];
		for(int i=0;i<26;i++) {
			if(ch[u][i]) {
				fail[ch[u][i]]=ch[fail[u]][i];
				q[++tl]=ch[u][i];
			} else ch[u][i]=ch[fail[u]][i];
		}
	}
}
int main() {
	scanf("%d",&n);
	for(int i=1;i<=n;i++) {
		scanf("%s",s+1);
		ins(strlen(s+1),i);
	}
	gfail(),scanf("%s",s+1),len=strlen(s+1);
	
	for(int i=1,u=0;i<=len;i++)u=ch[u][s[i]-'a'],sz[u]++;
	for(int i=tl;i;i--)sz[fail[q[i]]]+=sz[q[i]];
	for(int i=1;i<=n;i++)printf("%d\n",sz[flg[i]]);
}

AC 自动机上 dp

不知道哪一位神仙发明的东西

主要和字符串的包含关系有关，一般的状态至少两维， $f_{i,j}$ 表示第 $i$ 步在自动机上节点 $j$

第一维在一些题目里可以省略。

Wireless Password

以 Wireless Password 为例，题目求包含 $k$ 个给定串的长度为 $n$ 的字符串个数。

建出自动机，自动机上节点 $j$ 包含的串就是 $fail$ 链上的串。

又因为 $k$ 很小，可以考虑状压，记 $flg_j$ 为节点 $j$ 包含的串的集合

设 $f_{i,j,k}$ ， $k$ 为当前包含的字符串集合。则 $f_{i+1,v,k\cup flg_v}\leftarrow f_{i,j,k}$ 。其中 $v$ 为节点 $j$ 的儿子

#include <cstdio>
#include <cstring>
#include <queue>
#include <cmath>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
const LL P = 20090717;
int n, m, K, ch[105][26], fail[105], flg[105], tot, f[30][105][1100];
char a[105];
inline void ins(int le, int pos) {
    register int u = 0;
    for (int i = 1, s; i <= le; i++) {
        s = a[i] - 'a';
        if (!ch[u][s]) {
            ch[u][s] = ++tot;
            memset(ch[tot], 0, sizeof(ch[tot]));
        }
        u = ch[u][s];
    }
    flg[u] = 1 << (pos - 1);
}
queue<int> Q;
inline void gf() {
    for (int i = 0; i < 26; i++)
        if (ch[0][i]) Q.push(ch[0][i]);
    for (int u; !Q.empty(); ) {
        u = Q.front(), Q.pop();
        flg[u] |= flg[fail[u]];
        for (int i = 0; i < 26; i++) {
            if (ch[u][i]) {
                fail[ch[u][i]] = ch[fail[u]][i];
                Q.push(ch[u][i]);
            } else ch[u][i] = ch[fail[u]][i];
        }
    }
}
int main() {
    while (scanf("%d%d%d", &n, &m, &K), n) {
        memset(ch[0], 0, sizeof(ch[0]));
        memset(fail, 0, sizeof(fail));
        memset(flg, 0, sizeof(flg));
        tot = 0;
        for (int i = 1; i <= m; i++) {
            scanf("%s", a + 1);
            ins(strlen(a + 1), i);
        }
        gf();
        memset(f, 0, sizeof(f));
        f[0][0][0] = 1;
        for (int i = 0; i < n; i++)
            for (int j = 0; j <= tot; j++)
                for (int s = 0; s < (1 << m); s++) {
                    if (!f[i][j][s]) continue;
                    for (int k = 0, v; k < 26; k++) {
                        v = ch[j][k];
                        (f[i + 1][v][s | flg[v]] += f[i][j][s]) %= P;
                    }
                }
        int ans = 0;
        for (int s = 0, t, l; s < (1 << m); s++) {
            for (l = 0, t = s; t; t -= t & -t, l++);
            if (l >= K) {
                for (int j = 0; j <= tot; j++)
                    (ans += f[n][j][s]) %= P;
            }
        }
        printf("%d\n", ans);
    }
}

DNA Sequence

求长度为 $n$ 的不包含给定串的字符串个数， $n\le 2\times 10^9$

同理，建自动机，如果 $j$ 的 $fail$ 链上有字符串，则点 $j$ 不能访问。

$f_{i+1,v}\leftarrow f_{i,j}$ ，需要满足， $v$ 能访问。

$n$ 有点大，但其实容易想出矩阵优化，从 0 出发走 $n$ 步的方案，将一步走到的点赋值，最终 $\sum a_{0,i}$

#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
const int P = 100000;
inline int id(char c) {
    if (c == 'A') return 0;
    if (c == 'C') return 1;
    if (c == 'T') return 2;
    return 3;
}
int n, K, ch[105][5], fail[105], flg[105], tot;
char a[15];
inline void ins(int le) {
    register int u = 0;
    for (int i = 1, s; i <= le; i++) {
        s = id(a[i]);
        if (!ch[u][s]) ch[u][s] = ++tot;
        u = ch[u][s];
    }
    flg[u] = 1;
}
struct mat {
    int a[105][105];
    mat() { memset(a, 0, sizeof(a)); }
    mat operator * (mat b) {
        mat c;
        for (int i = 0; i <= tot; i++)
            for (int j = 0; j <= tot; j++)
                for (int k = 0; k <= tot; k++)
                    (c.a[i][j] += 1ll * a[i][k] * b.a[k][j] % P) %= P;
        return c;
    }
} ;
queue<int> Q;
inline void GF() {
    for (int i = 0; i < 4; i++)
        if (ch[0][i]) Q.push(ch[0][i]);
    for (int u; !Q.empty(); ) {
        u = Q.front(), Q.pop();
        flg[u] |= flg[fail[u]];
        for (int i = 0; i < 4; i++) {
            if (ch[u][i]) {
                fail[ch[u][i]] = ch[fail[u]][i];
                Q.push(ch[u][i]);
            } else ch[u][i] = ch[fail[u]][i];
        }
    }
}
int main() {
    while (scanf("%d%d", &n, &K) != EOF) {
        tot = 0;
        memset(fail, 0, sizeof(fail));
        memset(ch, 0, sizeof(ch));
        memset(flg, 0, sizeof(flg));
        for (int i = 1; i <= n; i++) {
            scanf("%s", a + 1);
            ins(strlen(a + 1));
        }
        GF();
        mat o, res;
        for (int i = 0; i <= tot; i++)
            for (int j = 0; j < 4; j++)
                if (!flg[ch[i][j]]) o.a[i][ch[i][j]]++;
        for (int i = 0; i <= tot; i++) res.a[i][i] = 1;
        for (; K; K >>= 1, o = o * o)
            if (K & 1) res = res * o;
        int ans = 0;
        for (int i = 0; i <= tot; i++) (ans += res.a[0][i]) %= P;
        printf("%d\n", ans);
    }
}

考研路茫茫——单词情结

hdu 2243

求长度不超过 $n$ 的包含给定串的字符串个数，可以用总数减去不包含的个数。

构造矩阵的方法同上，区别是要求 $A+A^2+\cdots+A^n$ ，这是矩阵的经典运用，分治 + 快速幂解决。

同理，总数为 $26+26^2+\cdots+26^n$ ，求法一样。

#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
int n, L, ch[35][26], fail[35], vis[35], tot;
char a[10];
struct mat {
    uLL a[35][35];
    mat() { memset(a, 0, sizeof(a)); }
    mat operator * (mat b) {
        mat c;
        for (int i = 0; i <= tot; i++)
            for (int j = 0; j <= tot; j++)
                for (int k = 0; k <= tot; k++)
                    c.a[i][j] += a[i][k] * b.a[k][j];
        return c;
    }
    mat operator + (mat b) {
        mat c;
        for (int i = 0; i <= tot; i++)
            for (int j = 0; j <= tot; j++)
                c.a[i][j] = a[i][j] + b.a[i][j];
        return c;
    }
};
inline void ins(int le) {
    register int u = 0;
    for (int i = 1, s; i <= le; i++) {
        s = a[i] - 'a';
        if (!ch[u][s]) ch[u][s] = ++tot;
        u = ch[u][s];
    }
    vis[u] = 1;
}
queue<int> Q;

inline void gf() {
    for (int i = 0; i < 26; i++)
        if (ch[0][i]) Q.push(ch[0][i]);
    for (int u; !Q.empty(); ) {
        u = Q.front(), Q.pop();
        vis[u] |= vis[fail[u]];
        for (int i = 0; i < 26; i++) {
            if (ch[u][i]) {
                fail[ch[u][i]] = ch[fail[u]][i];
                Q.push(ch[u][i]);
            } else ch[u][i] = ch[fail[u]][i];
        }
    }
}
mat Pow(mat x, int y) {
    mat res;
    for (int i = 0; i <= tot; i++) res.a[i][i] = 1;
    for (; y; y >>= 1, x = x * x)
        if (y & 1) res = res * x;
    return res;
}
mat cal(mat a, int n) {
    if (n == 1) return a;
    mat res = cal(a, n >> 1);
    if (n & 1) {
        mat t = Pow(a, n / 2 + 1);
        res = (res + (t * res)) + t;
    } else {
        mat t = Pow(a, n / 2);
        res = res + (t * res);
    }
    return res;
}
uLL Pow(uLL x, int y) {
    uLL res = 1;
    for (; y; y >>= 1, x = x * x)
        if (y & 1) res = res * x;
    return res;
}
uLL cal(uLL a, int n) {
    if (n == 1) return a;
    uLL res = cal(a, n >> 1);
    if (n & 1) {
        uLL t = Pow(a, n / 2 + 1);
        res = res + (t * res) + t;
    } else {
        uLL t = Pow(a, n / 2);
        res = res + (t * res);
    }
    return res;
}
int main() {
    while (scanf("%d%d", &n, &L) != EOF) {
        tot = 0;
        memset(ch, 0, sizeof(ch));
        memset(fail, 0, sizeof(fail));
        memset(vis, 0, sizeof(vis));
        for (int i = 1; i <= n; i++) {
            scanf("%s", a + 1);
            ins(strlen(a + 1));
        }
        gf();
        mat st;
        for (int i = 0; i <= tot; i++)
            for (int j = 0; j < 26; j++)
                if (!vis[ch[i][j]]) st.a[i][ch[i][j]]++;
        // for (int i = 0; i <= tot; i++, puts(""))
        //     for (int j = 0; j <= tot; j++) cout << st.a[i][j] << ' ';
        uLL tmp = cal(26, L);
        mat res = cal(st, L);
        for (int i = 0; i <= tot; i++)
            tmp -= res.a[0][i];
        printf("%llu\n", tmp);
    }
}

Lost's revenge

给定 $n$ 个模式串，要求文本串重组后包含最多模式串个数。

字符串只包含 A,T,G,C ，可以用四维状态表示一个字符串。

其实没有必要，文本串长度最多为 40，

用一个类似哈希的数组 $h_{i,j,k,l}$ 表示 $i$ 个 A ， $j$ 个 C ， $k$ 个 G ， $l$ 个 T 的状态编号。

没有必要记录长度， $f_{j,s}$ 表示在 $j$ 号点，状态为 $s$ ， $s$ 最多为 40

#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
int n, Tk, tot, ch[505][4], fail[505], cnt[505], o[4], h[45][45][45][45], f[505][15000];
char a[55];
inline int id(char c) {
    if (c == 'A') return 0;
    if (c == 'C') return 1;
    if (c == 'G') return 2;
    return 3;
}
inline void ins(int le) {
    register int u = 0;
    for (int i = 1, s; i <= le; i++) {
        s = id(a[i]);
        if (!ch[u][s]) ch[u][s] = ++tot;
        u = ch[u][s];
    }
    ++cnt[u];
}
queue<int> Q;
inline void gf() {
    for (int i = 0; i < 4; i++)
        if (ch[0][i]) Q.push(ch[0][i]);
    for (int u; !Q.empty(); ) {
        u = Q.front(), Q.pop();
        cnt[u] += cnt[fail[u]];
        for (int i = 0; i < 4; i++) {
            if (ch[u][i]) {
                fail[ch[u][i]] = ch[fail[u]][i];
                Q.push(ch[u][i]);
            } else ch[u][i] = ch[fail[u]][i];
        }
    }
}
int main() {
    while (scanf("%d", &n), n) {
        memset(ch, 0, sizeof(ch));
        memset(fail, 0, sizeof(fail));
        memset(cnt, 0, sizeof(cnt));
        tot = 0;
        for (int i = 1; i <= n; i++) {
            scanf("%s", a + 1);
            ins(strlen(a + 1));
        }
        gf();
        scanf("%s", a + 1);
        memset(o, 0, sizeof(o));
        int le = strlen(a + 1);
        for (int i = 1; i <= le; i++)
            o[id(a[i])]++;
        int pos = 0;
        for (int i = 0; i <= o[0]; i++)
            for (int j = 0; j <= o[1]; j++)
                for (int k = 0; k <= o[2]; k++)
                    for (int l = 0; l <= o[3]; l++)
                        h[i][j][k][l] = pos++;
        memset(f, -1, sizeof(f));
        f[0][0] = 0;
        for (int A = 0; A <= o[0]; A++)
            for (int C = 0; C <= o[1]; C++)
                for (int G = 0; G <= o[2]; G++)
                    for (int T = 0; T <= o[3]; T++) {
                        int s = h[A][C][G][T];
                        int nw[4] = { A, C, G, T };
                        for (int j = 0; j <= tot; j++)
                            for (int k = 0, v, ns; k < 4; k++) {
                                if (nw[k] == o[k] || f[j][s] == -1) continue;
                                nw[k]++;
                                v = ch[j][k], ns = h[nw[0]][nw[1]][nw[2]][nw[3]];
                                f[v][ns] = max(f[v][ns], f[j][s] + cnt[v]);
                                nw[k]--;
                            }
                    }
        int ans = 0;
        for (int i = 0; i <= tot; i++)
            ans = max(ans, f[i][pos - 1]);
        printf("Case %d: %d\n", ++Tk, ans);
    }
}

总结

AC 自动机是一个有力的工具，应在做题中深入理解

本文作者：小蒟蒻laf

本文链接：https://www.cnblogs.com/KonjakLAF/p/14860486.html

posted @ 2021-06-07 20:42 小蒟蒻laf 阅读(76) 评论(0) 收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

公告

昵称：小蒟蒻laf 园龄：5年2个月粉丝：24 关注：3

昵称：小蒟蒻laf
园龄： 5年2个月
粉丝： 24
关注： 3

2025年5月

日

一

二

三

四

五

六

小蒟蒻laf

漫漫 OI 路

AC 自动机

AC 自动机

fail

查询

trie 图

Code

Fail 树

一些灵活应用

AC 自动机上 dp

Wireless Password

DNA Sequence

考研路茫茫——单词情结

Lost's revenge

总结

公告

搜索

常用链接

最新随笔

积分与排名

随笔分类

随笔档案

阅读排行榜

推荐排行榜

最新评论