偏差和方差
期望
在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和。它反映随机变量平均取值的大小。 大数定律规定,随着重复次数接近无穷大,数值的算术平均值几乎肯定地收敛于期望值。
方差(variance)
方差用来衡量随机变量或一组数据的离散程度。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。描述的是预测值的变化范围,离散程度,也就是离其期望值的距离。方差越大,数据的分布越分散。
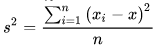
其中x为该组数据的平均值
离散型:
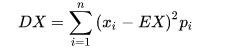
连续型:
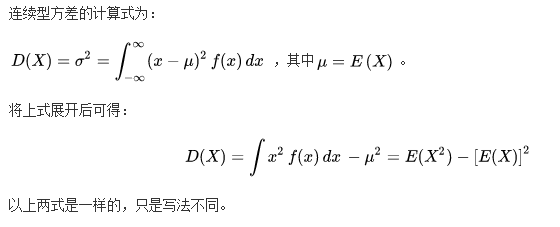
偏差bias
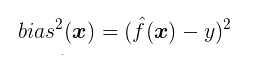
学习能力不行造成的误差是偏差,学习能力太强造成的误差是方差。方差,是形容数据分散程度的,算是“无监督的”,客观的指标,偏差,形容数据跟我们期望的中心差得有多远,算是“有监督的”,有人的知识参与的指标。




· 如何把ASP.NET Core WebApi打造成Mcp Server
· Linux系列:如何用perf跟踪.NET程序的mmap泄露
· 日常问题排查-空闲一段时间再请求就超时
· Java虚拟机代码是如何一步一步变复杂且难以理解的?
· 领域驱动的事实与谬误 一 DDD 与 MVC
· 如何把ASP.NET Core WebApi打造成Mcp Server
· 排行榜的5种实现方案!
· 在 .NET 中使用 Sqids 快速的为数字 ID 披上神秘短串,轻松隐藏敏感数字!
· 突破Excel百万数据导出瓶颈:全链路优化实战指南
· ChatGPT为何放弃WebSocket?揭秘EventSource的三大决胜优势