对条件概率的理解

条件概率定义

对条件概率的定义最初起源于离散事件，事件A和事件B的发生之间存在什么关系。在事件A发生的情况下，有多大的概率事件B可以发生？

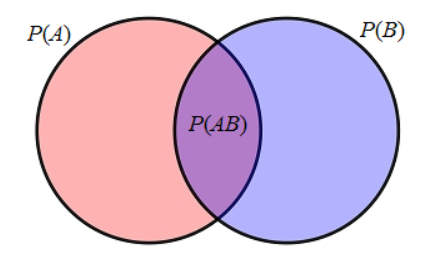
从上边的图片分析，就是当我知道自己在右边紫色的圈中，我同样还有粉色成分的概率是多少？
注意这个前提，我在紫色圈中。这是一个已知的信息，借用参考链接2中的一句话：条件概率的本质是额外信息导致你要考虑的样本空间范围的减少。
【A和B同时发生本来要在整个空间中寻找，条件概率直接定位在紫色空间中寻找】
再结合我们常用的全概率公式，可以看出条件概率的本质就是划块 在给定信息的条件下，对新事物的理解会发生什么样的变化？

贝叶斯公式

提到条件概率就不得不说贝叶斯公式

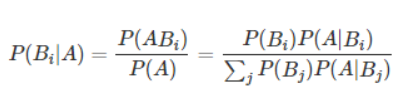
贝叶斯公式就是已知结果发生了，反过来研究造成事件发生的原因。

我们从通常推理的角度来解释这个式子
如果你知道事件$A$发生了，现在想知道是什么造成的？首先要罗列所有的原因（可能与该事件发生有关的所有$B_i$），然后找到这些原因$B_i$和事件$A$之间的关系【它们对事件$A$发生可能会有多大的贡献】。正常情况下我们直接排序就可以知道最有可能的是谁了。数学嘛 喜欢把这些东西都归一化 用一个更加统一的形式表示，就变成了上述贝叶斯公式的形式。
著名的三门问题就是如此，仔细想想 获得哪个门后边无奖励会对你的决策作出什么影响呢？

那么扩展到离散、连续分布呢？

条件分布

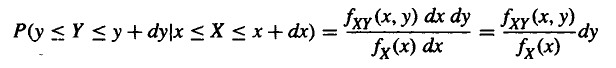
上式最右边的表达式可解释为$x$固定时$y$的函数，分子是联合密度$f_{xy}(x,y)$，视为固定$x$时$y$的函数。
可将其理解为沿着X轴方向用垂直与x轴的面来切割联合函数。
剖面上出现的曲线表示了条件概率函数的走向，利用分母将其积分校正到1。

扩展到具体的分布上，如何理解那些先验分布、似然函数和后验分布呢？

先验、后验和似然

（贝叶斯推断）
在搜集任何数据之前，采用先验密度来刻画我们对似然函数中未知参数的认知。$\pi (p)$
实际去做实验，用似然函数来刻画实际的结果。当使用的样本和实验的结果固定后，似然函数就成了以参数为未知量的函数。$f(x|\pi(p))$
后验分布就是根据实验的结果修正我们对未知参数的认知，从均匀到不均匀，逐步定位 找到准确的估计。$f(p|x)$

参考链接：

1. 如何形象地理解条件概率及运算公式？ - 王赟 Maigo的回答 - 知乎 https://www.zhihu.com/question/29155526/answer/88287808

2. 到底要如何理解条件概率？ - segABC的回答 - 知乎 https://www.zhihu.com/question/322520602/answer/673611140

3. 如何理解条件概率？ - 身高163的回答 - 知乎 https://www.zhihu.com/question/27462939/answer/410847522